误差函数

互补误差函数，记为 erfc，在误差函数的基础上定义：

${\displaystyle {\mbox{erfc}}(x)=1-{\mbox{erf}}(x)={\frac {2}{\sqrt {\pi }}}\int _{x}^{\infty }e^{-t^{2}}\,\mathrm {d} t\,.}$

虚误差函数，记为 erfi，定义为：

${\displaystyle \operatorname {erfi} (z)=-i\,\,\operatorname {erf} (i\,z).}$

複誤差函數，记为w(z)，也在误差函数的基础上定义：

${\displaystyle w(z)=e^{-z^{2}}{\textrm {erfc}}(-iz).}$

误差函数来自测度论，后来与测量误差无关的其他领域也用到这一函数，但仍然使用误差函数这一名字。

误差函数与标准正态分布的积分累积分布函数${\displaystyle \Phi }$ 的关系为^[2]

${\displaystyle \Phi (x)={\frac {1}{2}}+{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right).}$

复平面上的图

Integrand exp(−z²)

erf(z)

误差函数是奇函数：

${\displaystyle \operatorname {erf} (-z)=-\operatorname {erf} (z)}$

对于任何 复数 z:

${\displaystyle \operatorname {erf} ({\overline {z}})={\overline {\operatorname {erf} (z)}}}$

其中 ${\displaystyle {\overline {z}}}$ 表示 z的 复共轭。

复平面上，函数 ƒ = exp(−z²) 和 ƒ = erf(z) 如图所示。粗绿线表示 Im(ƒ) = 0，粗红线表示 Im(ƒ) < 0， 粗蓝线为 Im(ƒ) > 0。细绿线表示 Im(ƒ) = constant，细红线表示 Re(ƒ) = constant<0，细蓝线表示 Re(ƒ) = constant>0。

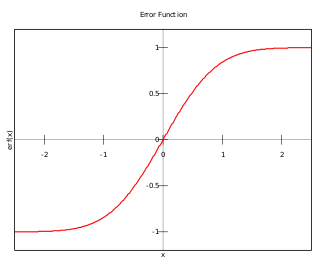
在实轴上， z → ∞时，erf(z) 趋于1，z → −∞时，erf(z) 趋于−1 。在虚轴上， erf(z) 趋于 ±i∞。

误差函数是整函数，没有奇点（无穷远处除外），泰勒展开收敛。

误差函数泰勒级数：

${\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{n!(2n+1)}}={\frac {2}{\sqrt {\pi }}}\left(z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{10}}-{\frac {z^{7}}{42}}+{\frac {z^{9}}{216}}-\ \cdots \right)}$

对每个复数 z均成立。上式可以用迭代形式表示：

${\displaystyle \operatorname {erf} (z)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }\left(z\prod _{k=1}^{n}{\frac {-(2k-1)z^{2}}{k(2k+1)}}\right)={\frac {2}{\sqrt {\pi }}}\sum _{n=0}^{\infty }{\frac {z}{2n+1}}\prod _{k=1}^{n}{\frac {-z^{2}}{k}}}$

误差函数的导数：

${\displaystyle {\frac {\rm {d}}{{\rm {d}}z}}\,\mathrm {erf} (z)={\frac {2}{\sqrt {\pi }}}\,e^{-z^{2}}.}$

误差函数的 不定积分为：

${\displaystyle z\,\operatorname {erf} (z)+{\frac {e^{-z^{2}}}{\sqrt {\pi }}}}$

逆误差函数 可由 麦克劳林级数表示：

${\displaystyle \operatorname {erf} ^{-1}(z)=\sum _{k=0}^{\infty }{\frac {c_{k}}{2k+1}}\left({\frac {\sqrt {\pi }}{2}}z\right)^{2k+1},\,\!}$

其中， c₀ = 1 ，

${\displaystyle c_{k}=\sum _{m=0}^{k-1}{\frac {c_{m}c_{k-1-m}}{(m+1)(2m+1)}}=\left\{1,1,{\frac {7}{6}},{\frac {127}{90}},{\frac {4369}{2520}},\ldots \right\}.}$

即：

${\displaystyle \operatorname {erf} ^{-1}(z)={\tfrac {1}{2}}{\sqrt {\pi }}\left(z+{\frac {\pi }{12}}z^{3}+{\frac {7\pi ^{2}}{480}}z^{5}+{\frac {127\pi ^{3}}{40320}}z^{7}+{\frac {4369\pi ^{4}}{5806080}}z^{9}+{\frac {34807\pi ^{5}}{182476800}}z^{11}+\cdots \right).\ }$

逆互补误差函数定义为：

${\displaystyle \operatorname {erfc} ^{-1}(1-z)=\operatorname {erf} ^{-1}(z).}$

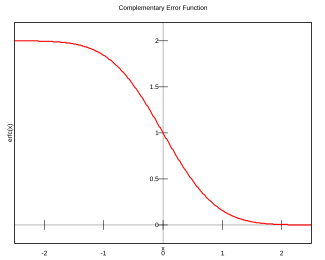
互补误差函数的渐近展开，

${\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\left[1+\sum _{n=1}^{\infty }(-1)^{n}{\frac {1\cdot 3\cdot 5\cdots (2n-1)}{(2x^{2})^{n}}}\right]={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}},\,}$

其中 (2n – 1)!! 为 双阶乘，x为实数，该级数对有限 x发散。对于${\displaystyle N\in \mathbb {N} }$ ，有

${\displaystyle \mathrm {erfc} (x)={\frac {e^{-x^{2}}}{x{\sqrt {\pi }}}}\sum _{n=0}^{N-1}(-1)^{n}{\frac {(2n-1)!!}{(2x^{2})^{n}}}+R_{N}(x)\,}$

其中余项用以 大O符号表示为

${\displaystyle R_{N}(x)=O(x^{-2N+1}e^{-x^{2}})}$ as ${\displaystyle x\to \infty }$ .

余项的精确形式为：

${\displaystyle R_{N}(x):={\frac {(-1)^{N}}{\sqrt {\pi }}}2^{-2N+1}{\frac {(2N)!}{N!}}\int _{x}^{\infty }t^{-2N}e^{-t^{2}}\,\mathrm {d} t,}$

对于比较大的 x, 只需渐近展开中开始的几项就可以得到 erfc(x)很好的近似值。

互补误差函数的连分式展开形式：^[3]

${\displaystyle \mathrm {erfc} (z)={\frac {z}{\sqrt {\pi }}}e^{-z^{2}}{\cfrac {a_{1}}{z^{2}+{\cfrac {a_{2}}{1+{\cfrac {a_{3}}{z^{2}+{\cfrac {a_{4}}{1+\dotsb }}}}}}}}\qquad a_{1}=1,\quad a_{m}={\frac {m-1}{2}},\quad m\geq 2.}$

${\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4})^{4}}}}$     (最大误差： 5·10⁻⁴)

其中， a₁ = 0.278393, a₂ = 0.230389, a₃ = 0.000972, a₄ = 0.078108

${\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+a_{3}t^{3})e^{-x^{2}},\quad t={\frac {1}{1+px}}}$     (最大误差：2.5·10⁻⁵)

其中， p = 0.47047, a₁ = 0.3480242, a₂ = −0.0958798, a₃ = 0.7478556

${\displaystyle \operatorname {erf} (x)\approx 1-{\frac {1}{(1+a_{1}x+a_{2}x^{2}+\cdots +a_{6}x^{6})^{16}}}}$     (最大误差： 3·10⁻⁷)

其中， a₁ = 0.0705230784, a₂ = 0.0422820123, a₃ = 0.0092705272, a₄ = 0.0001520143, a₅ = 0.0002765672, a₆ = 0.0000430638

${\displaystyle \operatorname {erf} (x)\approx 1-(a_{1}t+a_{2}t^{2}+\cdots +a_{5}t^{5})e^{-x^{2}},\quad t={\frac {1}{1+px}}}$     (最大误差： 1.5·10⁻⁷)

其中， p = 0.3275911, a₁ = 0.254829592, a₂ = −0.284496736, a₃ = 1.421413741, a₄ = −1.453152027, a₅ = 1.061405429

以上所有近似式适用范围是： x ≥ 0. 对于负的 x, 误差函数是奇函数这一性质得到误差函数的值， erf(x) = −erf(−x).

另有近似式：

${\displaystyle \operatorname {erf} (x)\approx \operatorname {sgn}(x){\sqrt {1-\exp \left(-x^{2}{\frac {4/\pi +ax^{2}}{1+ax^{2}}}\right)}}}$

其中，

${\displaystyle a={\frac {8(\pi -3)}{3\pi (4-\pi )}}\approx 0.140012.}$

该近似式在0或无穷的邻域非常准确，x整个定义域上，近似式最大误差小于0.00035，取 a ≈ 0.147 ，最大误差可减小到0.00012。^[4]

逆误差函数近似式:

${\displaystyle \operatorname {erf} ^{-1}(x)\approx \operatorname {sgn}(x){\sqrt {{\sqrt {\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)^{2}-{\frac {\ln(1-x^{2})}{a}}}}-\left({\frac {2}{\pi a}}+{\frac {\ln(1-x^{2})}{2}}\right)}}.}$

下式在整个定义域上，最大误差可低至 ${\displaystyle 1.2\cdot 10^{-7}}$ ：^[5]

${\displaystyle \operatorname {erf} (x)={\begin{cases}1-\tau &\mathrm {for\;} x\geq 0\\\tau -1&\mathrm {for\;} x<0\end{cases}}}$

其中，

${\displaystyle {\begin{array}{rcl}\tau &=&t\cdot \exp \left(-x^{2}-1.26551223+1.00002368\cdot t+0.37409196\cdot t^{2}+0.09678418\cdot t^{3}\right.\\&&\qquad -0.18628806\cdot t^{4}+0.27886807\cdot t^{5}-1.13520398\cdot t^{6}+1.48851587\cdot t^{7}\\&&\qquad \left.-0.82215223\cdot t^{8}+0.17087277\cdot t^{9}\right)\end{array}}}$

${\displaystyle t={\frac {1}{1+0.5\,|x|}}}$

误差函数本质上与标准正态累积分布函数${\displaystyle \Phi }$ 是等价的，

${\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{\tfrac {-t^{2}}{2}}\,\mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]={\frac {1}{2}}\,\operatorname {erfc} \left(-{\frac {x}{\sqrt {2}}}\right)}$

可整理为如下形式：

${\displaystyle {\begin{aligned}\mathrm {erf} (x)&=2\Phi \left(x{\sqrt {2}}\right)-1\\\mathrm {erfc} (x)&=2\Phi \left(-x{\sqrt {2}}\right)=2\left(1-\Phi \left(x{\sqrt {2}}\right)\right).\end{aligned}}}$

${\displaystyle \Phi }$ 的逆函数为正态分位函数，即概率单位（英语：Probit）函数，

${\displaystyle \operatorname {probit} (p)=\Phi ^{-1}(p)={\sqrt {2}}\,\operatorname {erf} ^{-1}(2p-1)=-{\sqrt {2}}\,\operatorname {erfc} ^{-1}(2p).}$

误差函数为标准正态分布的尾概率Q函数（英语：Q-function）的关系为，

${\displaystyle Q(x)={\frac {1}{2}}-{\frac {1}{2}}\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right).}$

误差函数是米塔-列夫勒函数的特例，可以表示为合流超几何函数，

${\displaystyle \mathrm {erf} (x)={\frac {2x}{\sqrt {\pi }}}\,_{1}F_{1}\left({\tfrac {1}{2}},{\tfrac {3}{2}},-x^{2}\right).}$

误差函数用正则Γ函数P和 不完全Γ函数表示为

${\displaystyle \operatorname {erf} (x)=\operatorname {sgn} (x)P\left({\tfrac {1}{2}},x^{2}\right)={\operatorname {sgn} (x) \over {\sqrt {\pi }}}\gamma \left({\tfrac {1}{2}},x^{2}\right).}$

${\displaystyle \scriptstyle \operatorname {sgn} (x)\ }$ 为 符号函数.

广义误差函数为：

${\displaystyle E_{n}(x)={\frac {n!}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{n}}\,\mathrm {d} t={\frac {n!}{\sqrt {\pi }}}\sum _{p=0}^{\infty }(-1)^{p}{\frac {x^{np+1}}{(np+1)p!}}\,.}$

其中，E₀(x)为通过原点的直线， ${\displaystyle \scriptstyle E_{0}(x)={\frac {x}{e{\sqrt {\pi }}}}}$ 。E₂(x) 即为误差函数 erf(x)。

x > 0时，广义误差函数可以用Γ函数和 不完全Γ函数表示，

${\displaystyle E_{n}(x)={\frac {\Gamma (n)\left(\Gamma \left({\frac {1}{n}}\right)-\Gamma \left({\frac {1}{n}},x^{n}\right)\right)}{\sqrt {\pi }}},\quad \quad x>0.\ }$

因此，误差函数可以用不完全Γ函数表示为：

${\displaystyle \operatorname {erf} (x)=1-{\frac {\Gamma \left({\frac {1}{2}},x^{2}\right)}{\sqrt {\pi }}}.\ }$

互补误差函数的迭代积分定义为：

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\int _{z}^{\infty }\mathrm {i} ^{n-1}\operatorname {erfc} \,(\zeta )\;\mathrm {d} \zeta .\,}$

可以展开成幂级数：

${\displaystyle \mathrm {i} ^{n}\operatorname {erfc} \,(z)=\sum _{j=0}^{\infty }{\frac {(-z)^{j}}{2^{n-j}j!\Gamma \left(1+{\frac {n-j}{2}}\right)}}\,,}$

满足如下对称性质：

${\displaystyle \mathrm {i} ^{2m}\operatorname {erfc} (-z)=-\mathrm {i} ^{2m}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}}}$

和

${\displaystyle \mathrm {i} ^{2m+1}\operatorname {erfc} (-z)=\mathrm {i} ^{2m+1}\operatorname {erfc} \,(z)+\sum _{q=0}^{m}{\frac {z^{2q+1}}{2^{2(m-q)-1}(2q+1)!(m-q)!}}\,.}$

• 古德温 - 斯塔顿积分

• MathWorld – Erf（页面存档备份，存于互联网档案馆）