Limit (mathematics)
In mathematics, a limit is the value that a function comes close to as the input comes close to some value.[1] When we use a function to solve a problem, sometimes certain values can not be used as inputs to the function, but we can see what the function comes close to when the input comes close to the value. Limits can be used to explain what happens in these cases.
Format
Limits are used to define many topics in calculus, like continuity, derivatives, and integrals.
For a function f, limit are written like this:

which reads "the limit of f of x, as x approaches c equals L". An alternative notation is "





For a sequence 

Example
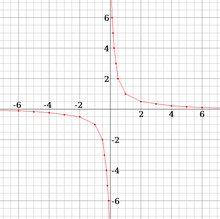
 . Note that the line doesn't touch 0 on either axis as
. Note that the line doesn't touch 0 on either axis as  is undefined.
is undefined.Imagine we have a function that takes an input, 


| x input | function | y output | x, y |
|---|---|---|---|
| 4 |  | 0.25 | 4, 0.25 |
| 3 |  | 0.33 | 3, 0.33 |
| 2 |  | 0.5 | 2, 0.5 |
| 1 |  | 1 | 1, 1 |
| 0 |  | undefined | 0, undefined |
As we can see here, division by zero is undefined. But if we look closer, then we can see that we still have valid output—as long as we never reach zero:
| x input | function | y output | x, y |
|---|---|---|---|
| 1 |  | 1 | 1, 1 |
| 0.5 |  | 2 | 0.5, 2 |
| 0.25 |  | 4 | 0.25, 4 |
| 0.125 |  | 8 | 0.125, 8 |
| -0.125 |  | -8 | -0.125, -8 |
| -0.25 |  | -4 | -0.25, -4 |
| -0.5 |  | -2 | -0.5, -2 |
| -1 |  | -1 | -1, -1 |
This problem is unique to zero as the function still works on every value up to zero, even if we approach from the negative side. As input numbers get arbitrarily small, the output will simply get arbitrarily large, and if we draw this on a graph, the line will stretch upwards without bound before it touches 0 on either axis.
One way we describe this is "The limit of 




Applications
While a limit cannot be reached, it can be approached to get a more accurate output value. For example, the mathematical constant 


| n input | function | output (e) |
|---|---|---|
| 1 |  | 2 |
| 10 |  | 2.5937424601 |
| 10,000 |  | 2.7182682372 |
| 10,000,000 |  | 2.71828169398... |
While the equation will never be equal to 





Related pages
- Limit of a sequence
- Cauchy sequence
- Limit of a function
- Big O notation: used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity