Anexo:Fractales por dimensión de Hausdorff

Según Falconer, una de las características esenciales de un fractal es que su dimensión de Hausdorff (δ) es estrictamente mayor que su dimensión topológica.^[1]Aquí se muestra una lista de fractales ordenados de forma creciente por su dimensión de Hausdorff, con el objetivo de visualizar qué significa que un fractal tenga una dimensión mayor o menor.

Fractales deterministas

δ (valor exacto)	δ (valor)	Nombre	Ilustración	Observaciones
$\textstyle {{\frac {\log(2)}{\log(\delta )}}?}$	0,4498?	Bifurcación de la curva logística		En el diagrama de bifurcaciones, al aproximarnos a la zona caótica, aparece una sucesión de periodos que se van duplicando en una progresión geométrica cuya razón tiende a 1/δ. (δ = constante de Feigenbaum = 4,6692)
$\textstyle {\frac {\log(2)}{\log(3)}}$	0,6309	Conjunto de Cantor		Se construye dividiendo cada segmento en tres y eliminando el de en medio en cada iteración. No es denso en ninguna parte y es un conjunto no numerable.
$\log {(1+{\sqrt {2}})}$	0,88137	Espectro del hamiltoniano de Fibonacci		El estudio del espectro del hamiltoniano de Fibonacci demuestra la existencia de cotas superiores e inferiores para su dimensión fractal, con lo que se muestra que el espectro converge a una constante determinada.^[2]
$\textstyle {1}$	1	Conjunto de Smith-Volterra-Cantor		Construido mediante la eliminación de un intervalo central de longitud $1/2^{2n}$ de cada uno de los intervalos existentes en la n-ésima iteración. No es denso en ninguna parte y tiene una medida de Lebesgue de ½.
$\textstyle {\frac {\log(8)}{\log(7)}}$	1,0686	Contorno de la isla de Gosper
Medida (recuento de cajas)	1,2	Conjunto de Julia Dendrita		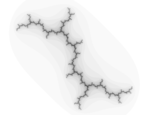Conjunto de Julia para los parámetros: Real = 0 e Imaginario = 1.
$\textstyle {3{\frac {\log(\phi )}{\log({\frac {3+{\sqrt {13}}}{2}})}}}$	1,2083	Fractal de Fibonacci (60°)		Construcción a partir de la palabra de Fibonacci.
	1,26	Atractor de Hénon		El atractor canónico de Hénon (con parámetros a = 1,4 y b = 0,3) tiene dimensión de Hausdorff δ = 1.261 ± 0.003. Distintos parámetros dan lugar a diferentes valores de δ.
$\textstyle {\frac {\log(4)}{\log(3)}}$	1,2619	Curva de Koch		Al yuxtaponer tres curvas de Koch se obtiene el copo de nieve (o bien el anti-copo de nieve) de Koch.
$\textstyle {\frac {\log(4)}{\log(3)}}$	1,2619	Frontera de la curva del terdragón		Sistema L: análogo a la curva del dragón con ángulo = 30°. El Fudgeflakese construye a partir de la yuxtaposición de tres segmentos iniciales en forma de triángulo.
$\textstyle {\frac {\log(4)}{\log(3)}}$	1,2619	Polvo de Cantor bidimensional		Conjunto de Cantor en 2D.
calculado	1,2683	Conjunto de Julia z²-1		Conjunto de Julia para c = -1.^[3]
	1,3057	Circunferencia de Apolonio		Véase^[4]
calculado	1,3934	Conejo de Douady		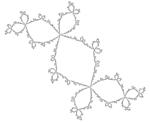Conjunto de Julia para c = -0,123 + 0,745i.^[5]
$\textstyle {\frac {\log(5)}{\log(3)}}$	1,4649	Fractal de Vicsek		Construido mediante la sustitución iterativa de un cuadrado por una cruz formada por cinco cuadrados.
$\textstyle {\frac {\log(5)}{\log(3)}}$	1,4649	Curva cuadrática de Koch (tipo 1)		Se puede reconocer en él el patrón del fractal de Vicsek.
$\textstyle {{\frac {\log(8)}{\log(4)}}={\frac {3}{2}}}$	1,5000	Curva cuadrática de Koch (tipo 2)		También conocido como "salchicha de Minkowski".
$\textstyle {\frac {\log \left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)}{\log(2)}}$	1,5236	Frontera de la curva del dragón		Cf Chang & Zhang.^[6]^[7]
$\textstyle {\frac {\log(3)}{\log(2)}}$	1,585	Árbol de tres ramas		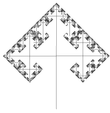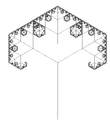Cada rama se divide en tres, en las imágenes con ángulos de 90° y 60°). La dimensión fractal del árbol es la dimensión fractal de las ramas terminales. NB: el árbol de dos ramas tiene una dimensión fractal de solo 1.
$\textstyle {\frac {\log(3)}{\log(2)}}$	1,585	Triángulo de Sierpinski		También es el triángulo de Pascal módulo 2.
$\textstyle {\frac {\log(3)}{\log(2)}}$	1,585	Curva de la punta de flecha de Sierpinski		Con el mismo límite que el triángulo (arriba), pero construido a partir de una curva unidimensional.
$\textstyle {1+{\frac {\log 2}{\log 3}}}$	1,6309	Triángulo de Pascal módulo 3		Para un triángulo módulo k, si k es primo, la dimensión fractal es $\scriptstyle {1+\log _{k}({\frac {k+1}{2}})}$ (Cf Stephen Wolfram^[8]).
$\textstyle {3{\frac {\log(\phi )}{\log(1+{\sqrt {2}})}}}$	1,6379	Fractal de Fibonacci		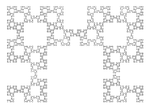Fractal basado en la palabra de Fibonacci (o sucesión de los conejos) Sloane A005614. Ilustración: Fractal tras 23 iteraciones (F23=28657 segmentos).^[9].
$\textstyle {1+{\frac {\log 3}{\log 5}}}$	1,6826	Triángulo de Pascal módulo 5		Para un triángulo módulo k, si k es primo, la dimensión fractal es $\scriptstyle {1+\log _{k}({\frac {k+1}{2}})}$ (Cf Stephen Wolfram^[8]).
$\textstyle {\frac {\log(4)}{\log({\sqrt {5}})}}$	1,7227	Fractal del molinete		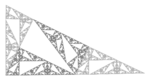Construido con el molinete (en inglés pinwheel) de Conway.
$\textstyle {\frac {\log(7)}{\log(3)}}$	1,7712	Hexacopo		En cada iteración se cambia cada hexágono por un copo de 7 hexágonos. Su frontera es el copo de von Koch y contiene infinitos copos de Koch (blancos y negros).
log (7)/log (3)	1.7712	Fractal H-I de Rivera	Imagen del Fractal H-I de Rivera	Se parte de un cuadrado unidad dividiendo sus dimensiones en tres partes iguales para formar con ellas nueve cuadrados autosimilares al primer cuadrado, se quitan dos cuadrados medios (el que está arriba y el que está abajo del cuadrado central), en cada uno de los siete cuadrados no eliminados se repite el proceso, así se continúa de manera indefinida.
$\textstyle {\frac {\log(4)}{\log(2(1+\cos(85^{\circ })))}}$	1,7848	Curva de von Koch a 85°, fractal de Cesàro		Generalización de la curva de von Koch con un ángulo a de entre 0 y 90°. La dimensión fractal es entonces $\scriptstyle {\frac {\log(4)}{\log(2(1+\cos(a)))}}$ . El fractal de Cesàro se basa en este patrón.
$\textstyle {\frac {\log(6)}{\log(1+\phi )}}$	1,8617	Pentacopo		En cada iteración se cambia cada pentágono por un copo de 6 pentágonos. $\phi$ = razón áurea = $\scriptstyle {\frac {1+{\sqrt {5}}}{2}}$ .
$\textstyle {\frac {\log(8)}{\log(3)}}$	1,8928	Alfombra de Sierpinski		Cada una de las caras de la esponja de Menger es una alfombra de Sierpinski, como lo es la superficie inferior de la superficie de Koch cuadrática tridimensional (tipo 1).
$\textstyle {\frac {\log(8)}{\log(3)}}$	1,8928	Polvo de Cantor tridimensional		Conjunto de Cantor en tres dimensiones.
Estimado	1,9340	Frontera de la curva de Lévy		Estimado por Duvall y Keesling (1999). La propia curva tiene una dimensión fractal de 2.
	1,974	Teselación de Penrose		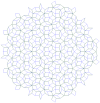See Ramachandrarao, Sinha & Sanyal^[10].
$\textstyle {2}$	2	Frontera del conjunto de Mandelbrot		La frontera y el propio conjunto tienen la misma dimensión^[11].
$\textstyle {2}$	2	Conjunto de Julia		Para determinados valores de c (incluido c perteneciente a la frontera del conjunto de Mandelbrot), el conjunto de Julia tiene una dimensión de 2.^[12].
$\textstyle {2}$	2	Curva de Sierpinski		Toda curva de Peano que llena el plano tiene una dimensión de Hausdorff de 2.
$\textstyle {2}$	2	Curva de Hilbert
$\textstyle {2}$	2	Curva de Peano		Así como una familia de curvas construidas de forma similar, como las curvas de Wunderlich.
$\textstyle {2}$	2	Curva de Moore		Se puede extender a 3 dimensiones.
	2	Curva de Lebesgue o de orden z		A diferencia de las anteriores, esta curva que llena el plano es diferenciable en casi todas partes. También se puede definir otro tipo en dos dimensiones. Al igual que la curva de Hilbert, se puede extender a tres dimensiones.^[13]
$\textstyle {{\frac {\log(2)}{\log({\sqrt {2}})}}=2}$	2	Curva del dragón		Su frontera tiene una dimensión fractal de 1,5236270862^[14].
	2	Curva del terdragón		L-sistema: F→F+F–F, ángulo=120°.
$\textstyle {{\frac {\log(4)}{\log(2)}}=2}$	2	T-cuadrado
$\textstyle {{\frac {\log(4)}{\log(2)}}=2}$	2	Curva de Gosper		Su frontera es la isla de Gosper.
$\textstyle {{\frac {\log(4)}{\log(2)}}=2}$	2	Tetraedro de Sierpinski		Cada tetraedro se sustituye por cuatro tetraedros.
$\textstyle {{\frac {\log(4)}{\log(2)}}=2}$	2	Fractal H		También el «árbol de Mandelbrot», que muestra un patrón similar.
$\textstyle {{\frac {\log(2)}{\log(2/{\sqrt {2}})}}=2}$	2	Árbol de Pitágoras		Cada cuadrado genera dos cuadrados con un cociente de reducción de ${\frac {\sqrt {2}}{2}}$ .
$\textstyle {{\frac {\log(4)}{\log(2)}}=2}$	2	Cruz griega fractal en 2D		Cada segmento es reemplazado por una cruz formada por 4 segmentos.
	2,06	Atractor de Lorenz		Para valores precisos de los parámetros.
$\textstyle {\frac {\log(20)}{\log(2+\phi )}}$	2,3296	Dodecaedro fractal		Cada dodecaedro es sustituido por 20 dodecaedros más pequeños.
$\textstyle {\frac {\log(13)}{\log(3)}}$	2,3347	Superficie cuadrática tridimensional de Koch (tipo 1)		Extensión tridimensional de la curva cuadrática de Koch (tipo 1). La ilustración muestra la segunda iteración.
	2.4739	Intersticios entre las esferas de Apolonio		Intersticios entre las esferas de Apolonio, equivalente tridimensional del círculo de Apolonio. Dimensión calculada por M. Borkovec, W. De Paris y R. Peikert.^[15]
$\textstyle {{\frac {\log(32)}{\log(4)}}={\frac {5}{2}}}$	2,50	Superficie cuadrática tridimensional de Koch (tipo 2)		Extensión tridimensional de la curva cuadrática de Koch (tipo 2). La ilustración muestra la segunda iteración
$\textstyle {\frac {\log(16)}{\log(3)}}$	2,5237	Teseracto de Cantor	no se puede representar	Conjunto de Cantor en cuatro dimensiones. Generalización: en un espacio de dimensión n, el conjunto de Cantor tiene una dimensión de Hausdorff de $\scriptstyle {n{\frac {\log(2)}{\log(3)}}}$ .
$\textstyle {\frac {\log(12)}{\log(1+\phi )}}$	2,5819	Icosaedro fractal		Cada icosaedro es sustituido por 12 icosaedros más pequeños.
$\textstyle {\frac {\log(6)}{\log(2)}}$	2,5849	Cruz griega fractal en 3D		Cada segmento es sustituido por una cruz tridimensional formada por 6 segmentos.
$\textstyle {\frac {\log(6)}{\log(2)}}$	2,5849	Octaedro fractal		Cada octaedro es sustituido por 6 octaedros más pequeños.
$\textstyle {\frac {\log(6)}{\log(2)}}$	2,5849	Superficie de Koch		Cada triángulo equilátero es sustituido por seis triángulos equiláteros de la mitad de tamaño.
$\textstyle {\frac {\log(20)}{\log(3)}}$	2,7268	Esponja de Menger		Y su superficie tiene una dimensión fractal de $\scriptstyle {{\frac {\log(12)}{\log(3)}}=2,2618}$ .
$\textstyle {{\frac {\log(8)}{\log(2)}}=3}$	3	Curva de Hilbert en 3D		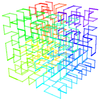Curva Hilbert extendida a 3 dimensiones.
$\textstyle {{\frac {\log(8)}{\log(2)}}=3}$	3	Curva de Lebesgue en 3D		Curva de Lebesgue extendida a 3 dimensiones.
$\textstyle {{\frac {\log(8)}{\log(2)}}=3}$	3	Curva de Moore en 3D		Curva de Moore extendida a 3 dimensiones.

Fractales aleatorios y naturales

δ (valor exacto)	δ (valor)	Nombre	Observaciones
Medido	1,24	Línea de costa de Gran Bretaña
$\textstyle {\frac {4}{3}}$	1,33	Frontera del movimiento browniano	(Cf Lawler, Schramm, Werner).^[16]
$\textstyle {\frac {4}{3}}$	1,33	Polímero en 2D	Similar al movimiento browniano en 2D sin autointersecciones. (Cf Sapoval).
$\textstyle {\frac {4}{3}}$	1,33	Frente de percolación o frente de corrosión en 2D	Dimensión fractal del frente de percolación por invasión en el umbral de percolación (59,3%). También es la dimensión fractal del frente de corrosión (Cf Sapoval).
	1,40	Agregado de agregados en 2D	Cuando se limitan por difusión, los agregados se combinan progresivamente para formar un agregado único de dimensión 1,4. (Cf Sapoval)
Medido	1,52	Línea de costa de Noruega	Véase J. Feder.^[17]
Medido	1,55	Camino aleatorio sin autointersecciones	Camino aleatorio sin autointersecciones en una malla cuadrada, pero con una rutina que permite volver atrás, para así evitar los caminos cortados.
$\textstyle {\frac {5}{3}}$	1,66	Polímero en 3D	De forma similar al movimiento browniano en una malla cúbica, pero sin autointersecciones (Cf Sapoval).
	1,70	Agregado por difusión en 2D	En 2 dimensiones, los agregados formados por agregación por difusión limitada muestran una dimensión fractal de alrededor de 1,70 (Cf Sapoval).
$\textstyle {\frac {91}{48}}$	1,8958	Agregado de percolación en 2D	Por debajo del umbral de percolación (59.3%) el agregado de percolación por invasión tiene una dimensión fractal de 91/48 (Cf Sapoval). Más allá de ese umbral, el agregado es infinito y 91/48 pasa a ser la dimensión fractal de los «claros».
$\textstyle {{\frac {\log(2)}{\log({\sqrt {2}})}}=2}$	2	Movimiento browniano	O movimiento aleatorio. La dimensión de Hausdorff es igual a 2 en 2D, en 3D y en todas las dimensiones mayores (K.Falconer "The geometry of fractal sets").
$\textstyle {\frac {\log(13)}{\log(3)}}$	2,33	Coliflor	Cada rama se divide en unas 13 ramas de un tercio de su tamaño.
	2,5	Bolas de papel	Cuando se forman bolas de papel de distinto tamaño pero formados del mismo tipo de papel y con la misma razón entre los lados, el diámetro de las bolas elevado a un exponente no entero comprendido entre 2 y 3 será aproximadamente proporcional al área de las hojas de las que se formaron dichas bolas. [1] Se formarán pliegues a cualquier escala.
	2,50	Agregado por difusión en 3D	En 3 dimensiones, los agregados formados por agregación por difusión limitada muestran una dimensión fractal de alrededor de 2,50 (Cf Sapoval).
	2,50	Figura de Lichtenberg	Su forma y crecimiento parecen estar relacionados con el proceso de agregación por difusión limitada (Cf Sapoval).
Medido	2,66	Brócoli	^[18]
	2,79	Superficie del cerebro humano	^[19]
	2,97	Superficie del pulmón	Los alveolos de un pulmón forman un fractal de superficie fractal próxima a 3 (Cf Sapoval).
Calculado	3	Cuerda cuántica	Dimensión de Hausdorff de una cuerda cuántica cuyo punto representativo vaga aleatoriamente.^[20]
$\textstyle {\log _{2}({f_{1}^{2}+f_{2}^{2}+f_{3}^{2}+f_{4}^{2}})}$	$\textstyle {\in (-\infty ,2)}$	Cascada multiplicativa	Este es un ejemplo de distribución multifractal, ya que no es exactamente autosimilar. Sin embargo, al elegir $\textstyle {f_{1},f_{2},f_{3},f_{4}}$ de una forma particular se puede forzar que la distribución se convierta en un monofractal^[21].

Véase también

Wikimedia Commons alberga una galería multimedia sobre fractales.
Dimensión fractal
Dimensión de Hausdorff
Invarianza de escala

Referencias

¹Kenneth Falconer, Fractal Geometry, John Wiley & Son Ltd; ISBN 0-471-92287-0 (March 1990)

Bibliografía

Benoît Mandelbrot, The Fractal Geometry of Nature, W. H. Freeman & Co; ISBN 0-7167-1186-9 (September 1982).
Heinz-Otto Peitgen, The Science of Fractal Images, Dietmar Saupe (editor), Springer Verlag, ISBN 0-387-96608-0 (August 1988)
Michael F. Barnsley, Fractals Everywhere, Morgan Kaufmann; ISBN 0-12-079061-0
Bernard Sapoval, « Universalités et fractales », collection Champs, Flammarion.

Enlaces externos

Algunos de los fractales anteriores con GeoGebra

En inglés:

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

Search