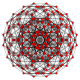
| Regular 5-orthoplex (pentacross) | |
|---|---|
 Orthogonal projection inside Petrie polygon | |
| Type | Regular 5-polytope |
| Family | orthoplex |
| Schläfli symbol | {3,3,3,4} {3,3,31,1} |
| Coxeter-Dynkin diagrams | |
| 4-faces | 32 {33} |
| Cells | 80 {3,3} |
| Faces | 80 {3} |
| Edges | 40 |
| Vertices | 10 |
| Vertex figure |  16-cell |
| Petrie polygon | decagon |
| Coxeter groups | BC5, [3,3,3,4] D5, [32,1,1] |
| Dual | 5-cube |
| Properties | convex, Hanner polytope |
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
It has two constructed forms, the first being regular with Schläfli symbol {33,4}, and the second with alternately labeled (checkerboarded) facets, with Schläfli symbol {3,3,31,1} or Coxeter symbol 211.
It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the 5-hypercube or 5-cube.
Alternate names
- pentacross, derived from combining the family name cross polytope with pente for five (dimensions) in Greek.
- Triacontaditeron (or triacontakaiditeron) - as a 32-facetted 5-polytope (polyteron).
As a configuration
This configuration matrix represents the 5-orthoplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-orthoplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]

Cartesian coordinates
Cartesian coordinates for the vertices of a 5-orthoplex, centered at the origin are
- (±1,0,0,0,0), (0,±1,0,0,0), (0,0,±1,0,0), (0,0,0,±1,0), (0,0,0,0,±1)
Construction
There are three Coxeter groups associated with the 5-orthoplex, one regular, dual of the penteract with the C5 or [4,3,3,3] Coxeter group, and a lower symmetry with two copies of 5-cell facets, alternating, with the D5 or [32,1,1] Coxeter group, and the final one as a dual 5-orthotope, called a 5-fusil which can have a variety of subsymmetries.
| Name | Coxeter diagram | Schläfli symbol | Symmetry | Order | Vertex figure(s) |
|---|---|---|---|---|---|
| regular 5-orthoplex |          | {3,3,3,4} | [3,3,3,4] | 3840 |        |
| Quasiregular 5-orthoplex |        | {3,3,31,1} | [3,3,31,1] | 1920 |      |
| 5-fusil | |||||
         | {3,3,3,4} | [4,3,3,3] | 3840 |        | |
         | {3,3,4}+{} | [4,3,3,2] | 768 |        | |
         | {3,4}+{4} | [4,3,2,4] | 384 |               | |
         | {3,4}+2{} | [4,3,2,2] | 192 |               | |
         | 2{4}+{} | [4,2,4,2] | 128 |        | |
         | {4}+3{} | [4,2,2,2] | 64 |               | |
         | 5{} | [2,2,2,2] | 32 |        |
Other images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph |  |  |  |
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph |  |  | |
| Dihedral symmetry | [4] | [4] |
 The perspective projection (3D to 2D) of a stereographic projection (4D to 3D) of the Schlegel diagram (5D to 4D) of the 5-orthoplex. 10 sets of 4 edges form 10 circles in the 4D Schlegel diagram: two of these circles are straight lines in the stereographic projection because they contain the center of projection. |
Related polytopes and honeycombs
| 2k1 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group | E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 =  = E8+ = E8+ | E10 =  = E8++ = E8++ | |||
| Coxeter diagram |      |      |        |          |            |              |                |                  | |||
| Symmetry | [3−1,2,1] | [30,2,1] | [[31,2,1]] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 384 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph |  |  |  |  |  |  | - | - | |||
| Name | 2−1,1 | 201 | 211 | 221 | 231 | 241 | 251 | 261 | |||
This polytope is one of 31 uniform 5-polytopes generated from the B5 Coxeter plane, including the regular 5-cube and 5-orthoplex.
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o4o - tac".
External links
- Olshevsky, George. "Cross polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary