In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family.
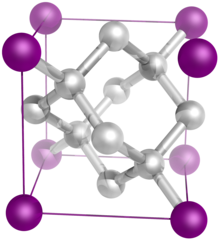
The seven crystal systems are triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. Informally, two crystals are in the same crystal system if they have similar symmetries (though there are many exceptions).
Classifications
Crystals can be classified in three ways: lattice systems, crystal systems and crystal families. The various classifications are often confused: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family".
Lattice system
A lattice system is a group of lattices with the same set of lattice point groups. The 14 Bravais lattices are grouped into seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic.
Crystal system
A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system. Of the 32 crystallographic point groups that exist in three dimensions, most are assigned to only one lattice system, in which case both the crystal and lattice systems have the same name. However, five point groups are assigned to two lattice systems, rhombohedral and hexagonal, because both exhibit threefold rotational symmetry. These point groups are assigned to the trigonal crystal system.
Crystal family
A crystal family is determined by lattices and point groups. It is formed by combining crystal systems that have space groups assigned to a common lattice system. In three dimensions, the hexagonal and trigonal crystal systems are combined into one hexagonal crystal family.

Comparison
Five of the crystal systems are essentially the same as five of the lattice systems. The hexagonal and trigonal crystal systems differ from the hexagonal and rhombohedral lattice systems. These are combined into the hexagonal crystal family.
The relation between three-dimensional crystal families, crystal systems and lattice systems is shown in the following table:
| Crystal family | Crystal system | Required symmetries of the point group | Point groups | Space groups | Bravais lattices | Lattice system |
|---|---|---|---|---|---|---|
| Triclinic | Triclinic | None | 2 | 2 | 1 | Triclinic |
| Monoclinic | Monoclinic | 1 twofold axis of rotation or 1 mirror plane | 3 | 13 | 2 | Monoclinic |
| Orthorhombic | Orthorhombic | 3 twofold axes of rotation or 1 twofold axis of rotation and 2 mirror planes | 3 | 59 | 4 | Orthorhombic |
| Tetragonal | Tetragonal | 1 fourfold axis of rotation | 7 | 68 | 2 | Tetragonal |
| Hexagonal | Trigonal | 1 threefold axis of rotation | 5 | 7 | 1 | Rhombohedral |
| 18 | 1 | Hexagonal | ||||
| Hexagonal | 1 sixfold axis of rotation | 7 | 27 | |||
| Cubic | Cubic | 4 threefold axes of rotation | 5 | 36 | 3 | Cubic |
| 6 | 7 | Total | 32 | 230 | 14 | 7 |
- Note: there is no "trigonal" lattice system. To avoid confusion of terminology, the term "trigonal lattice" is not used.
Crystal classes
The 7 crystal systems consist of 32 crystal classes (corresponding to the 32 crystallographic point groups) as shown in the following table below:
| Crystal family | Crystal system | Point group / Crystal class | Schönflies | Hermann–Mauguin | Orbifold | Coxeter | Point symmetry | Order | Abstract group |
|---|---|---|---|---|---|---|---|---|---|
| triclinic | pedial | C1 | 1 | 11 | [ ]+ | enantiomorphic polar | 1 | trivial  | |
| pinacoidal | Ci (S2) | 1 | 1x | [2,1+] | centrosymmetric | 2 | cyclic  | ||
| monoclinic | sphenoidal | C2 | 2 | 22 | [2,2]+ | enantiomorphic polar | 2 | cyclic  | |
| domatic | Cs (C1h) | m | *11 | [ ] | polar | 2 | cyclic  | ||
| prismatic | C2h | 2/m | 2* | [2,2+] | centrosymmetric | 4 | Klein four  | ||
| orthorhombic | rhombic-disphenoidal | D2 (V) | 222 | 222 | [2,2]+ | enantiomorphic | 4 | Klein four  | |
| rhombic-pyramidal | C2v | mm2 | *22 | [2] | polar | 4 | Klein four  | ||
| rhombic-dipyramidal | D2h (Vh) | mmm | *222 | [2,2] | centrosymmetric | 8 |  | ||
| tetragonal | tetragonal-pyramidal | C4 | 4 | 44 | [4]+ | enantiomorphic polar | 4 | cyclic  | |
| tetragonal-disphenoidal | S4 | 4 | 2x | [2+,2] | non-centrosymmetric | 4 | cyclic  | ||
| tetragonal-dipyramidal | C4h | 4/m | 4* | [2,4+] | centrosymmetric | 8 |  | ||
| tetragonal-trapezohedral | D4 | 422 | 422 | [2,4]+ | enantiomorphic | 8 | dihedral  | ||
| ditetragonal-pyramidal | C4v | 4mm | *44 | [4] | polar | 8 | dihedral  | ||
| tetragonal-scalenohedral | D2d (Vd) | 42m or 4m2 | 2*2 | [2+,4] | non-centrosymmetric | 8 | dihedral  | ||
| ditetragonal-dipyramidal | D4h | 4/mmm | *422 | [2,4] | centrosymmetric | 16 |  | ||
| hexagonal | trigonal | trigonal-pyramidal | C3 | 3 | 33 | [3]+ | enantiomorphic polar | 3 | cyclic  |
| rhombohedral | C3i (S6) | 3 | 3x | [2+,3+] | centrosymmetric | 6 | cyclic  | ||
| trigonal-trapezohedral | D3 | 32 or 321 or 312 | 322 | [3,2]+ | enantiomorphic | 6 | dihedral  | ||
| ditrigonal-pyramidal | C3v | 3m or 3m1 or 31m | *33 | [3] | polar | 6 | dihedral  | ||
| ditrigonal-scalenohedral | D3d | 3m or 3m1 or 31m | 2*3 | [2+,6] | centrosymmetric | 12 | dihedral  | ||
| hexagonal | hexagonal-pyramidal | C6 | 6 | 66 | [6]+ | enantiomorphic polar | 6 | cyclic  | |
| trigonal-dipyramidal | C3h | 6 | 3* | [2,3+] | non-centrosymmetric | 6 | cyclic  | ||
| hexagonal-dipyramidal | C6h | 6/m | 6* | [2,6+] | centrosymmetric | 12 |  | ||
| hexagonal-trapezohedral | D6 | 622 | 622 | [2,6]+ | enantiomorphic | 12 | dihedral  | ||
| dihexagonal-pyramidal | C6v | 6mm | *66 | [6] | polar | 12 | dihedral  | ||
| ditrigonal-dipyramidal | D3h | 6m2 or 62m | *322 | [2,3] | non-centrosymmetric | 12 | dihedral  | ||
| dihexagonal-dipyramidal | D6h | 6/mmm | *622 | [2,6] | centrosymmetric | 24 |  | ||
| cubic | tetartoidal | T | 23 | 332 | [3,3]+ | enantiomorphic | 12 | alternating  | |
| diploidal | Th | m3 | 3*2 | [3+,4] | centrosymmetric | 24 |  | ||
| gyroidal | O | 432 | 432 | [4,3]+ | enantiomorphic | 24 | symmetric  | ||
| hextetrahedral | Td | 43m | *332 | [3,3] | non-centrosymmetric | 24 | symmetric  | ||
| hexoctahedral | Oh | m3m | *432 | [4,3] | centrosymmetric | 48 |  | ||
The point symmetry of a structure can be further described as follows. Consider the points that make up the structure, and reflect them all through a single point, so that (x,y,z) becomes (−x,−y,−z). This is the 'inverted structure'. If the original structure and inverted structure are identical, then the structure is centrosymmetric. Otherwise it is non-centrosymmetric. Still, even in the non-centrosymmetric case, the inverted structure can in some cases be rotated to align with the original structure. This is a non-centrosymmetric achiral structure. If the inverted structure cannot be rotated to align with the original structure, then the structure is chiral or enantiomorphic and its symmetry group is enantiomorphic.[1]
A direction (meaning a line without an arrow) is called polar if its two-directional senses are geometrically or physically different. A symmetry direction of a crystal that is polar is called a polar axis.[2] Groups containing a polar axis are called polar. A polar crystal possesses a unique polar axis (more precisely, all polar axes are parallel). Some geometrical or physical property is different at the two ends of this axis: for example, there might develop a dielectric polarization as in pyroelectric crystals. A polar axis can occur only in non-centrosymmetric structures. There cannot be a mirror plane or twofold axis perpendicular to the polar axis, because they would make the two directions of the axis equivalent.
The crystal structures of chiral biological molecules (such as protein structures) can only occur in the 65 enantiomorphic space groups (biological molecules are usually chiral).
Bravais lattices
There are seven different kinds of lattice systems, and each kind of lattice system has four different kinds of centerings (primitive, base-centered, body-centered, face-centered). However, not all of the combinations are unique; some of the combinations are equivalent while other combinations are not possible due to symmetry reasons. This reduces the number of unique lattices to the 14 Bravais lattices.
The distribution of the 14 Bravais lattices into 7 lattice systems is given in the following table.
| Crystal family | Lattice system | Point group (Schönflies notation) | 14 Bravais lattices | |||
|---|---|---|---|---|---|---|
| Primitive (P) | Base-centered (S) | Body-centered (I) | Face-centered (F) | |||
| Triclinic (a) | Ci | 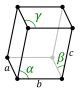 aP | ||||
| Monoclinic (m) | C2h |  mP |  mS | |||
| Orthorhombic (o) | D2h |  oP |  oS | 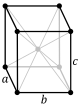 oI |  oF | |
| Tetragonal (t) | D4h |  tP |  tI | |||
| Hexagonal (h) | Rhombohedral | D3d |  hR | |||
| Hexagonal | D6h |  hP | ||||
| Cubic (c) | Oh | 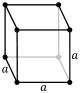 cP |  cI |  cF | ||
In geometry and crystallography, a Bravais lattice is a category of translative symmetry groups (also known as lattices) in three directions.
Such symmetry groups consist of translations by vectors of the form
- R = n1a1 + n2a2 + n3a3,
where n1, n2, and n3 are integers and a1, a2, and a3 are three non-coplanar vectors, called primitive vectors.
These lattices are classified by the space group of the lattice itself, viewed as a collection of points; there are 14 Bravais lattices in three dimensions; each belongs to one lattice system only. They[clarification needed] represent the maximum symmetry a structure with the given translational symmetry can have.
All crystalline materials (not including quasicrystals) must, by definition, fit into one of these arrangements.
For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3, or 4 larger than the primitive cell. Depending on the symmetry of a crystal or other pattern, the fundamental domain is again smaller, up to a factor 48.
The Bravais lattices were studied by Moritz Ludwig Frankenheim in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais in 1848.
In other dimensions
Two-dimensional space
Two dimensional space has the same number of crystal systems, crystal families, and lattice systems. In 2D space, there are four crystal systems: oblique, rectangular, square, and hexagonal.
Four-dimensional space
The four-dimensional unit cell is defined by four edge lengths (a, b, c, d) and six interaxial angles (α, β, γ, δ, ε, ζ). The following conditions for the lattice parameters define 23 crystal families
| No. | Family | Edge lengths | Interaxial angles |
|---|---|---|---|
| 1 | Hexaclinic | a ≠ b ≠ c ≠ d | α ≠ β ≠ γ ≠ δ ≠ ε ≠ ζ ≠ 90° |
| 2 | Triclinic | a ≠ b ≠ c ≠ d | α ≠ β ≠ γ ≠ 90° δ = ε = ζ = 90° |
| 3 | Diclinic | a ≠ b ≠ c ≠ d | α ≠ 90° β = γ = δ = ε = 90° ζ ≠ 90° |
| 4 | Monoclinic | a ≠ b ≠ c ≠ d | α ≠ 90° β = γ = δ = ε = ζ = 90° |
| 5 | Orthogonal | a ≠ b ≠ c ≠ d | α = β = γ = δ = ε = ζ = 90° |
| 6 | Tetragonal monoclinic | a ≠ b = c ≠ d | α ≠ 90° β = γ = δ = ε = ζ = 90° |
| 7 | Hexagonal monoclinic | a ≠ b = c ≠ d | α ≠ 90° β = γ = δ = ε = 90° ζ = 120° |
| 8 | Ditetragonal diclinic | a = d ≠ b = c | α = ζ = 90° β = ε ≠ 90° γ ≠ 90° δ = 180° − γ |
| 9 | Ditrigonal (dihexagonal) diclinic | a = d ≠ b = c | α = ζ = 120° β = ε ≠ 90° γ ≠ δ ≠ 90° cos δ = cos β − cos γ |
| 10 | Tetragonal orthogonal | a ≠ b = c ≠ d | α = β = γ = δ = ε = ζ = 90° |
| 11 | Hexagonal orthogonal | a ≠ b = c ≠ d | α = β = γ = δ = ε = 90°, ζ = 120° |
| 12 | Ditetragonal monoclinic | a = d ≠ b = c | α = γ = δ = ζ = 90° β = ε ≠ 90° |
| 13 | Ditrigonal (dihexagonal) monoclinic | a = d ≠ b = c | α = ζ = 120° β = ε ≠ 90° γ = δ ≠ 90° cos γ = −1/2cos β |
| 14 | Ditetragonal orthogonal | a = d ≠ b = c | α = β = γ = δ = ε = ζ = 90° |
| 15 | Hexagonal tetragonal | a = d ≠ b = c | α = β = γ = δ = ε = 90° ζ = 120° |
| 16 | Dihexagonal orthogonal | a = d ≠ b = c | α = ζ = 120° β = γ = δ = ε = 90° |
| 17 | Cubic orthogonal | a = b = c ≠ d | α = β = γ = δ = ε = ζ = 90° |
| 18 | Octagonal | a = b = c = d | α = γ = ζ ≠ 90° β = ε = 90° δ = 180° − α |
| 19 | Decagonal | a = b = c = d | α = γ = ζ ≠ β = δ = ε cos β = −1/2 − cos α |
| 20 | Dodecagonal | a = b = c = d | α = ζ = 90° β = ε = 120° γ = δ ≠ 90° |
| 21 | Diisohexagonal orthogonal | a = b = c = d | α = ζ = 120° β = γ = δ = ε = 90° |
| 22 | Icosagonal (icosahedral) | a = b = c = d | α = β = γ = δ = ε = ζ cos α = −1/4 |
| 23 | Hypercubic | a = b = c = d | α = β = γ = δ = ε = ζ = 90° |
The names here are given according to Whittaker.[3] They are almost the same as in Brown et al.,[4] with exception for names of the crystal families 9, 13, and 22. The names for these three families according to Brown et al. are given in parentheses.
The relation between four-dimensional crystal families, crystal systems, and lattice systems is shown in the following table.[3][4] Enantiomorphic systems are marked with an asterisk. The number of enantiomorphic pairs is given in parentheses. Here the term "enantiomorphic" has a different meaning than in the table for three-dimensional crystal classes. The latter means, that enantiomorphic point groups describe chiral (enantiomorphic) structures. In the current table, "enantiomorphic" means that a group itself (considered as a geometric object) is enantiomorphic, like enantiomorphic pairs of three-dimensional space groups P31 and P32, P4122 and P4322. Starting from four-dimensional space, point groups also can be enantiomorphic in this sense.
| No. of crystal family | Crystal family | Crystal system | No. of crystal system | Point groups | Space groups | Bravais lattices | Lattice system |
|---|---|---|---|---|---|---|---|
| I | Hexaclinic | 1 | 2 | 2 | 1 | Hexaclinic P | |
| II | Triclinic | 2 | 3 | 13 | 2 | Triclinic P, S | |
| III | Diclinic | 3 | 2 | 12 | 3 | Diclinic P, S, D | |
| IV | Monoclinic | 4 | 4 | 207 | 6 | Monoclinic P, S, S, I, D, F | |
| V | Orthogonal | Non-axial orthogonal | 5 | 2 | 2 | 1 | Orthogonal KU |
| 112 | 8 | Orthogonal P, S, I, Z, D, F, G, U | |||||
| Axial orthogonal | 6 | 3 | 887 | ||||
| VI | Tetragonal monoclinic | 7 | 7 | 88 | 2 | Tetragonal monoclinic P, I | |
| VII | Hexagonal monoclinic | Trigonal monoclinic | 8 | 5 | 9 | 1 | Hexagonal monoclinic R |
| 15 | 1 | Hexagonal monoclinic P | |||||
| Hexagonal monoclinic | 9 | 7 | 25 | ||||
| VIII | Ditetragonal diclinic* | 10 | 1 (+1) | 1 (+1) | 1 (+1) | Ditetragonal diclinic P* | |
| IX | Ditrigonal diclinic* | 11 | 2 (+2) | 2 (+2) | 1 (+1) | Ditrigonal diclinic P* | |
| X | Tetragonal orthogonal | Inverse tetragonal orthogonal | 12 | 5 | 7 | 1 | Tetragonal orthogonal KG |
| 351 | 5 | Tetragonal orthogonal P, S, I, Z, G | |||||
| Proper tetragonal orthogonal | 13 | 10 | 1312 | ||||
| XI | Hexagonal orthogonal | Trigonal orthogonal | 14 | 10 | 81 | 2 | Hexagonal orthogonal R, RS |
| 150 | 2 | Hexagonal orthogonal P, S | |||||
| Hexagonal orthogonal | 15 | 12 | 240 | ||||
| XII | Ditetragonal monoclinic* | 16 | 1 (+1) | 6 (+6) | 3 (+3) | Ditetragonal monoclinic P*, S*, D* | |
| XIII | Ditrigonal monoclinic* | 17 | 2 (+2) | 5 (+5) | 2 (+2) | Ditrigonal monoclinic P*, RR* | |
| XIV | Ditetragonal orthogonal | Crypto-ditetragonal orthogonal | 18 | 5 | 10 | 1 | Ditetragonal orthogonal D |
| 165 (+2) | 2 | Ditetragonal orthogonal P, Z | |||||
| Ditetragonal orthogonal | 19 | 6 | 127 | ||||
| XV | Hexagonal tetragonal | 20 | 22 | 108 | 1 | Hexagonal tetragonal P | |
| XVI | Dihexagonal orthogonal | Crypto-ditrigonal orthogonal* | 21 | 4 (+4) | 5 (+5) | 1 (+1) | Dihexagonal orthogonal G* |
| 5 (+5) | 1 | Dihexagonal orthogonal P | |||||
| Dihexagonal orthogonal | 23 | 11 | 20 | ||||
| Ditrigonal orthogonal | 22 | 11 | 41 | ||||
| 16 | 1 | Dihexagonal orthogonal RR | |||||
| XVII | Cubic orthogonal | Simple cubic orthogonal | 24 | 5 | 9 | 1 | Cubic orthogonal KU |
| 96 | 5 | Cubic orthogonal P, I, Z, F, U | |||||
| Complex cubic orthogonal | 25 | 11 | 366 | ||||
| XVIII | Octagonal* | 26 | 2 (+2) | 3 (+3) | 1 (+1) | Octagonal P* | |
| XIX | Decagonal | 27 | 4 | 5 | 1 | Decagonal P | |
| XX | Dodecagonal* | 28 | 2 (+2) | 2 (+2) | 1 (+1) | Dodecagonal P* | |
| XXI | Diisohexagonal orthogonal | Simple diisohexagonal orthogonal | 29 | 9 (+2) | 19 (+5) | 1 | Diisohexagonal orthogonal RR |
| 19 (+3) | 1 | Diisohexagonal orthogonal P | |||||
| Complex diisohexagonal orthogonal | 30 | 13 (+8) | 15 (+9) | ||||
| XXII | Icosagonal | 31 | 7 | 20 | 2 | Icosagonal P, SN | |
| XXIII | Hypercubic | Octagonal hypercubic | 32 | 21 (+8) | 73 (+15) | 1 | Hypercubic P |
| 107 (+28) | 1 | Hypercubic Z | |||||
| Dodecagonal hypercubic | 33 | 16 (+12) | 25 (+20) | ||||
| Total | 23 (+6) | 33 (+7) | 227 (+44) | 4783 (+111) | 64 (+10) | 33 (+7) | |
See also
- Crystal cluster – Group of crystals formed in an open space with form determined by their internal crystal structure
- Crystal structure – Ordered arrangement of atoms, ions, or molecules in a crystalline material
- List of space groups
- Polar point group – symmetry in geometry and crystallography
References
Works cited
- Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. International Tables for Crystallography. Vol. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.
External links

- Overview of the 32 groups
- Mineral galleries – Symmetry
- all cubic crystal classes, forms, and stereographic projections (interactive java applet)
- Crystal system at the Online Dictionary of Crystallography
- Crystal family at the Online Dictionary of Crystallography
- Lattice system at the Online Dictionary of Crystallography
- Conversion Primitive to Standard Conventional for VASP input files Archived 2021-11-26 at the Wayback Machine
- Learning Crystallography