বক্রতার ব্যাসার্ধ
ব্যবকলনীয় জ্যামিতিতে বক্রতার ব্যাসার্ধ R বক্রতার বিপরীত (reciprocal) রাশি। একটি বক্ররেখার কোন বিন্দুতে বক্রতার ব্যাসার্ধ হল ঐ বিন্দুর চুম্বনকারী বৃত্ত বা আপতিত বৃত্তের (Osculating cirle) ব্যাসার্ধ।[১] প্রকৃতপক্ষে কোন বিন্দুতে বক্রতার ব্যাসার্ধ চুম্বনকারী বৃত্তের ব্যাসার্ধের পুরোপুরি সমান না হয়ে খুবই কাছাকাছি মানের হয়ে থাকে। তাই বলা যায়, একটি বক্ররেখার কোন বিন্দুতে সর্বাধিক নিখুঁত বা কাছাকাছি মানের যে বৃত্ত আঁকা যায় সেই বৃত্তের যে ব্যাসার্ধ, সেটিই ঐ বিন্দুতে বক্ররেখাটির বক্রতার ব্যাসার্ধ। অন্যভাবে, একটি বক্ররেখার কোন বিন্দুতে বক্রতার ব্যাসার্ধ ঐ বিন্দুতে বক্ররেখাটির বক্রতার সর্বোচ্চ সন্নিকটবর্তী বৃত্তচাপটির ব্যাসার্ধের সমান। একইভাবে, পৃষ্ঠতলের বক্রতার ব্যাসার্ধ পৃষ্ঠতলটির সাধারণ ছেদক বা ছেদকসমূহের সাথে যে বৃত্তটি সর্বোচ্চ পরিমাণে মিলে যায় সেই বৃত্তের ব্যাসার্ধের সমান।[২][৩][৪] (একটি নির্দিষ্ট বিন্দুতে একটি পৃষ্ঠতলের সাধারণ ছেদক হচ্ছে ঐ পৃষ্ঠতলের সাথে একটি সাধারণ তলের পারস্পরিক ছেদের ফলে উৎপন্ন বক্ররেখা[৫][৬][৭])। বক্ররেখা বরাবর এগোতে থাকলে বক্রতার ব্যাসার্ধের পরিবর্তন হতে থাকবে।
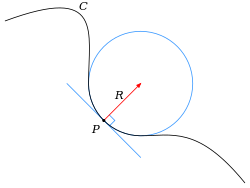

সংজ্ঞা
স্থানিক বক্ররেখার ক্ষেত্রে বক্রতা ভেক্টরের (curvature vector) দৈর্ঘ্যই বক্রতার ব্যাসার্ধ। সমতলিক বক্ররেখার ক্ষেত্রে বক্রতার ব্যাসার্ধ R হল নিম্নোক্ত রাশির পরম মান[৪]—
যেখানে s হল বক্ররেখার উপরস্থ নির্দিষ্ট কোন বিন্দু থেকে চাপ দৈর্ঘ্য, φ হল স্পর্শকীয় কোণ এবং κ হল বক্রতা।
সূত্র
দ্বিমাত্রিকের ক্ষেত্রে
কার্তেসীয় স্থানাংক ব্যবস্থায় বক্ররেখাকে y(x) আকারে লেখা হলে বক্রতার ব্যাসার্ধ (বক্ররেখাকে দুবার পর্যন্ত ব্যবকলনযোগ্য ধরে):—
এবং | z | হল zএর পরম মান।বক্ররেখাটিকে x(t) এবং y(t) এর মাধ্যমে পরামিতিকরণ করা হলে বক্রতার ব্যাসার্ধ:—
পরীক্ষণ ও ভুলকরণ পদ্ধতিতে(Heuristically) একে নিম্নরূপে লেখা যায়[৩]:—
n মাত্রিকের ক্ষেত্রে
যদি γ : ℝ → ℝn বক্ররেখাটি ℝn-এ পরামিতিকৃত হলে বক্ররেখার প্রত্যেক বিন্দুতে বক্রতার ব্যাসার্ধ ρ : ℝ → ℝ, is given by[৪]
- যেখানে—
বিশেষ ক্ষেত্রে f(t), ℝ থেকে ℝ-এ কোন ফাংশন হলে এবং এর লেখচিত্র γ(t) = (t, f(t)) হলে লেখচিত্রটির বক্রতার ব্যাসার্ধ:—
প্রতিপাদন
γ কে উপরের ন্যায় এবং t কে নির্দিষ্ট ধরা যাক। পরামিতিকৃত একটি বৃত্তের ব্যাসার্ধ ρ নির্ণয় করতে হবে যা t-তে γ এর শূন্যতম, প্রথম ও দ্বিতীয় অন্তরজের সদৃশ হবে। স্পষ্টতই নির্ণেয় ব্যাসার্ধ অবস্থান γ(t) এর উপর নির্ভরশীল নয়, এটি শুধু বেগ γ′(t) এবং ত্বরণ γ″(t) এর উপর নির্ভরশীল হবে। v এবং w ভেক্টর দুটি থেকে শুধু তিনটি স্বাধীন স্কেলার ভেক্টর পাওয় যায়। যথা:- v · v, v · w, and w · w। একইভাবে বক্রতার ব্যাসার্ধকে অবশ্যই | γ′(t) |2, | γ″(t) |2 এবং γ′(t) · γ″(t) এই তিনটি স্কেলাররের ফাংশন হতে হবে।[৪]
ℝn-এ পরামিতিকৃত কোন বৃত্তের জন্য সাধারণ সমীকরণটি হল—
যেখানে c ∈ ℝn হচ্ছে বৃত্তটির কেন্দ্র (অন্তরজে এটি দৃশ্যমান না হওয়ায় অপ্রাসঙ্গিক)। a,b ∈ ℝn হচ্ছে দৈর্ঘ্য ρ এর লম্ব ভেক্টর ( a · a = b · b = ρ2 ও a · b = 0) এবং h : ℝ → ℝ হচ্ছে t-তে দুবার ব্যবকলনযোগ্য একটি অবাধ (arbitrary) ফাংশন।
g সংশ্লিষ্ট অন্তরজসমূহকে নিম্নরূপভাবে পাওয়া যাবে—
g এর অন্তরজগুলোকে t-তে γ এর অনুরূপ অন্তরজগুলোর সমান ধরে পাই—
ρ, h′(t) এবং h″(t) অজানা রাশিযুক্ত এই সমীকরণত্রয়কে ρ এর জন্য সমাধান করা যেতে পারে এবং বক্রতার ব্যাসার্ধের নিম্নোক্ত সূত্র পাওয়া যেতে পারে:—
অথবা পড়ার সুবিধার্থে t পরামিতি বর্জন করে নিম্নোক্তভাবে:—
উদাহরণ
অর্ধবৃত্ত ও বৃত্ত
অর্ধ-তল হচ্ছে অসীম দৈর্ঘ্যের একটি সরলরেখার যেকোন এক পাশের সমস্ত বিন্দু নিয়ে (রেখার অপর পাশের বিন্দুগুলো অবশ্যই বর্জনীয়) কল্পিত একটি সমতলীয় অঞ্চল। সহজভাবে বলা যায়, কোন সমতলের উপর অসীম দৈর্ঘ্যের একটি রেখা আঁকা হলে রেখাটির যেকোন এক পাশে সমতলটির যে খণ্ডিত অংশ পাওয়া যাবে তাই অর্ধ-তল। রেখাস্থ বিন্দুসমূহকে অর্ধ-তলটির অন্তর্ভুক্ত করা হলে একে বদ্ধ অর্ধ-তল এবং রেখাস্থ বিন্দুসমূহকে অন্তর্ভুক্ত করা না হলে একে খোলা অর্ধ-তল বলা হয়।[৮][৯]
ঊর্ধ্বস্থ অর্ধ-তলে a ব্যাসার্ধের অর্ধ-বৃত্তের জন্য—
এবং নিম্নস্থ অর্ধ-তলে a ব্যাসার্ধের অর্ধ-বৃত্তের জন্য—
এখন a ব্যাসার্ধের বৃত্তের যে বক্রতার ব্যাসার্ধ পাব তা হবে a এর সমান।
উপবৃত্ত

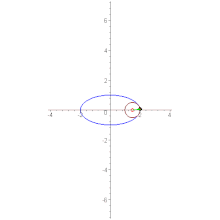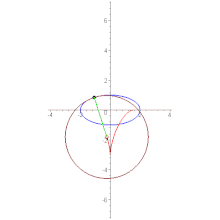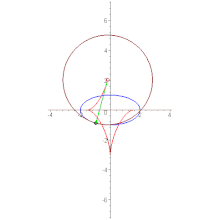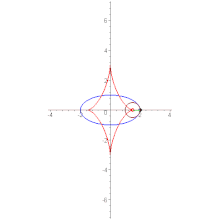
2a বৃহৎ অক্ষ ও 2b ক্ষুদ্র অক্ষযুক্ত উপবৃত্তের বৃহৎ অক্ষের শীর্ষ বিন্দু দুটিতে বক্রতার ব্যাসার্ধ ক্ষুদ্রতম হবে (R = +b২/a) পক্ষান্তরে ক্ষুদ্র অক্ষের শীর্ষ বিন্দু দুটিতে বক্রতার ব্যাসার্ধ হবে সর্বোচ্চ (R = +a২/b)।
বক্ররেখা বরাবর এগোতে থাকলে বক্রতার ব্যাসার্ধ তথা বক্রতার কেন্দ্রের অবস্থানের পরিবর্তন হতে থাকে। একটি বক্ররেখার বক্রতার কেন্দ্রগুলোর জন্য যে লোকাস পাওয়া যায় তা বক্ররেখাটির ইভলিউট গঠন করে।












